Un polinomio es una expresión algebraica formada por la suma de un número finito de monomios.
P(x) = an xn + an-1 xn-1 + ··· + a2 x2 + a1 x + a0
Donde, n es un número natural y Coeficientes: a_n, a_{n-1},... ,a_1, a0, Variable o indeterminada: x, Coeficiente principal: a_n y Término independiente: a0. El coeficiente a de la mayor potencia de x es el coeficiente principal del polinomio. Ejemplos de polinomios:
En el primer ejemplo el exponente de es negativo contradiciendo la definición de polinomio, de igual forma en el ejemplo c donde el exponente de no es entero.
En el ejemplo b tenemos una expresión racional o fraccionaria con un polinomio en el numerador y otro en el denominador. El criterio que utilizaremos es el siguiente si el polinomio del denominador no es el constante o de grado cero, la expresión no es un polinomio. Recuerde que los exponentes deben ser enteros positivos.
Grado de un Polinomio
El grado de un polinomio P(x) es el mayor exponente al que se encuentra elevada la variable x. Según su grado los polinomios pueden ser de:
Tipos de polinomios
1. Polinomio nulo: Es aquel polinomio que tiene todos sus coeficientes nulos.
3. Polinomio heterogéneo: Es aquel polinomio en el que no todos sus términos no son del mismo grado.
4. Polinomio completo: Es aquel polinomio que tiene todos los términos desde el término independiente hasta el término de mayor grado.
5. Polinomio incompleto: Es aquel polinomio que no tiene todos los términos desde el término independiente hasta el término de mayor grado.
6. Polinomio ordenado: Un polinomio está ordenado si los monomios que lo forman están escritos de mayor a menor grado o inversamente.7. Polinomios iguales: Dos polinomios son iguales si verifican: Los dos polinomios tienen el mismo grado y si los coeficientes de los términos del mismo grado son iguales.
8. Polinomios semejantes: Es el resultado que obtenemos al sustituir la variable x por un número cualquiera. Dos polinomios son semejantes si verifican que tienen la misma parte literal.
9. Polinomio mónico: Un polinomio es mónico si su coeficiente principal es 1, por ejemplo:
Valor numérico de un polinomio: Es el resultado que obtenemos al sustituir la variable x por un número cualquiera. Ejemplo: Calcular el valor numérico del polinomio: P(x) = 2x^3+ 5x - 3, para los valores.
Ejemplos:
Suma: Sumamos términos semejantes es decir sumamos aquellos términos cuyas variables y exponentes sean iguales. Los pasos para hacer las suma son:
- Paso 1: Elimine los paréntesis
- Paso 2: Agrupe términos semejantes
- Paso 3: Sume y reste los términos semejantes.
Resta: Funciona igual que la suma solo hay que tener en cuenta que el signo negativo antes de los paréntesis cambia el signo de los términos dentro del paréntesis.
Ejemplo: Resta los siguientes polinomios:
- Paso 2: Elimine los paréntesis. Para hacerlo sólo escriba los términos que están dentro del paréntesis con sus signos correspondientes e ignore el signo + entre los dos paréntesis.
- Paso 3: Agrupe los términos semejantes; es decir los términos con iguales variables e iguales exponentes.
- Paso 4: Sume y reste los términos semejantes.
Así que aplicando este concepto a la expresión original tendríamos:
Multiplicación: Para multiplicar dos polinomios: multiplica cada término de un polinomio por cada término del otro polinomio. suma las respuestas, y simplifica si hace falta.
- Producto de monomios: Para multiplicar monomios debemos seguir los siguientes pasos: (2x2) . (3x)=
- Multiplicar los coeficientes. 2 . 3=6- Multiplicar la parte literal (las letras que aparecen en los monomios).
De esta modo, (2x2) . (3x)= 6x3
- Producto de polinomios: se obtiene multiplicando cada término del primero por el segundo y reduciendo luego los términos semejantes. De este modo obtenemos el polinomio resultante.
Ejemplos:
(2x+1).(3x+2)= 2x.(3x+2)+1.(3x+2)= 6x2+4x+3x+2=6x2(+4x+3x)+2=6x2+7x+2
(x-1).(x+2)=x.(x+2)-1.(x+2)= x2+2x-x-2=+x2(+2x-x)-2=x2+x-2
(3x+3).(x2+2x+1)= 3x.( x2+2x+1)+3.( x2+2x+1)= (3x3+6x2+3x)+(3x2+6x+3) = 3x3+9x2+9x+3
Por tanto, si nos encontramos con polinomios de más términos, ejemplo:
- P(x)= 2x2+5x-6
- Q(x)= 3x2-6x+3
División: En álgebra, la división de polinomios (también división polinomial o división polinómica) es un algoritmo que permite dividir un polinomio por otro polinomio que no sea nulo.
- División de monomios: Para dividir dos monomios debemos seguir los siguientes pasos: (15x2) / (3x)=
- Dividir los coeficientes. 15: 3=5
- Dividir la parte literal (las letras que aparecen en los monomios).
De esta modo, (15x2) / (5x)= 3x
Ejemplos:
8 a / 2 a = (8/2).(a/a)= 4
15 ay /3a = (15/3) (a.y)/ a = 5 y
12 bxy / -2 bxy = (12/-2) (b.x.y)/(bxy.) = -6
-6 v2 . c. x/-3vc= (-6/-3) (v2 .c. x) /(v. c) = 2 v
- División de un polinomio por un monomio: La división de un polinomio por un monomio (sólo si es posible) se obtiene dividiendo cada término del polinomio por el monomio, obteniendo como resultado otro polinomio. Ejemplo:
- División exacta de polinomios: En una división exacta de polinomios, el resto es igual a cero. Dividir el polinomio D(x) entre el polinomio d(x) es hallar otro polinomio cociente c(x) tal que multiplicado por el divisor dé el dividendo. Para realizar la división debemos actuar del mismo modo que la división entera de números naturales.
Vemos el siguiente ejemplo:
- P(x)= 3x3+13x2-13x+2
- V(x)= 3x-2
Realizar la siguiente operación: (3x3+13x2-13x+2): (3x-2)=
Así: C(x)=x2-5x+1 y R(x)=0 , en esta caso se dice que la división es exacta,
- División entera de polinomios: el resto es distinto de cero. En las divisiones enteras (o inexactas), el dividendo D(x) no es múltiplo del divisor d(x), y siempre se va a cumplir la propiedad fundamental de la división:
El grado del polinomio resto R(x) es siempre menor que el grado del polinomio divisor d(x).









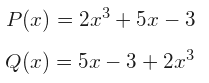

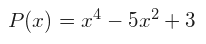




















No hay comentarios:
Publicar un comentario